Calculating Magnitude Of 3d Vectors

If a 3 5 6 and b 4 1 3 find the length ab.

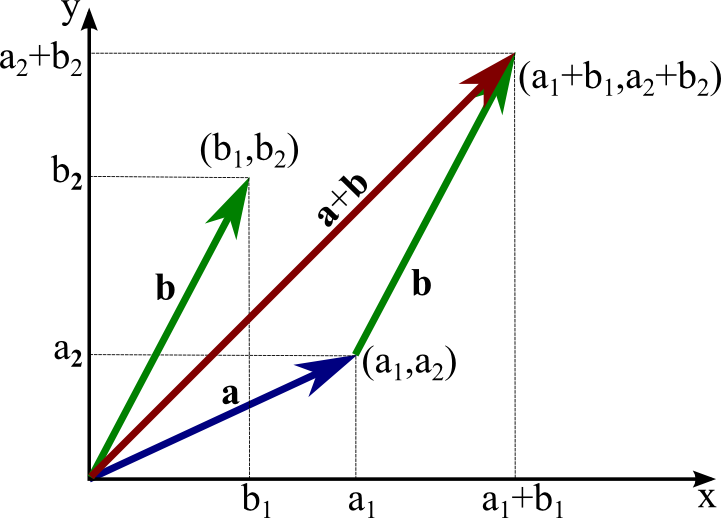
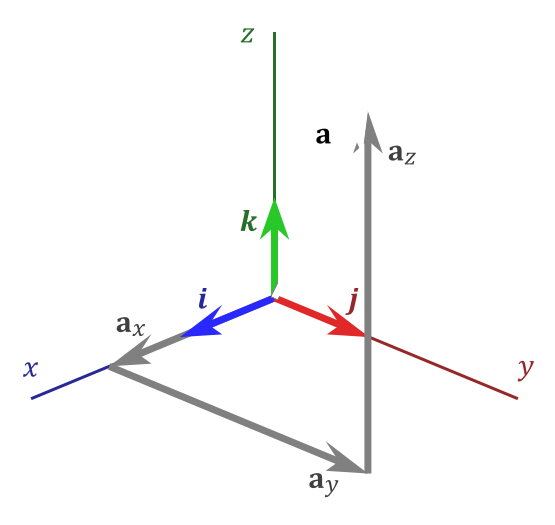
Calculating magnitude of 3d vectors. The notation for absolute value. The magnitude of the vector is equal to the hypotenuse of the triangle so you can use the pythagorean theorem to calculate it. All the 3d vectors can be represented in 3 dimensional space by a directed line segment which has a starting point and an ending point. Magnitude of a vector 3d.

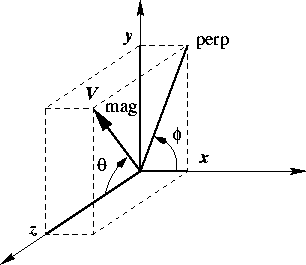
The 3d vectors are using the x y z axes. Either way the meaning is. Example 2 dot product using magnitude and angle. α is the angle between u and the x axis.

Find the dot product of the vectors p and q given that the angle between the two vectors is 35 and. By the way some textbooks represent magnitude with double bars. Rotate to landscape screen format on a mobile phone or small tablet to use the mathway widget a free math problem solver that answers your questions with step by step explanations. The pythagorean theorem is a 2 b 2 c 2.

Use thi online 3d vector magnitude calculator to calculate the magnitude of three dimensional vectors with the given vector coordinates. You can use the free mathway calculator and. Dot product of 3 dimensional vectors. Magnitude of vectors proof of pythagoras theorem all 3d vectors can be represented by a directed line segment in 3d space r3 which has a start point and an end point.

Calculating the magnitude of vectors is essential for all sorts of problems where forces collide. Calculate the angle of three dimensional vectors 3d vectors with entered vector coordinates. Cartesian xyz coordinates two vectors in 3d vector cross product vector addition and subtraction geometrically it is the product of the euclidean magnitudes of the two vectors and the cosine of the angle between them. The vector op has initial point at the origin o 0 0 0 and.

If r x y z represents the vector displacement of point r from the. 3 rearrange the pythagorean theorem to calculate the magnitude. β is the angle between u and the y axis. The 3d vectors are using the x y z axes.

3d vector magnitude calculate of magnitude of a 3 dimensional vector. Is also used for the magnitude of a vector. Calculate the magnitude of three dimensional vectors 3d vectors for entered vector coordinates. Magnitude is defined as the length of a vector.

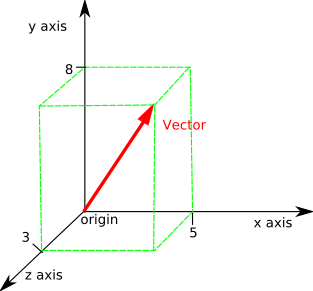
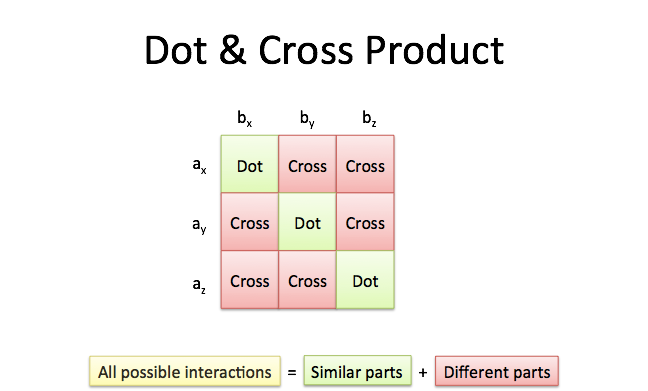
For example v refers to magnitude of the vector v. The vector op has initial point at the origin o 0 0 0 and terminal point at p 2 4 5. To find the dot product or scalar product of 3 dimensional vectors we just extend the ideas from the dot product in 2 dimensions that we met earlier. This gives each vector a magnitude the length of the line segment and direction from the start point to the end point.

Example of magnitude of a 3 dimensional vector. Find the magnitude of a 4i 3j 2k 2. This gives each vector a magnitude and direction.